Next: Conservative Vector Fields and Up: Line Integrals Previous: With respect to arc Contents
Here we are trying to compute integrals of the form
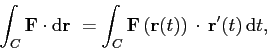

Let's work with the vector field
![]() . We will integrate along the curve
. We will integrate along the curve ![]() parameterized by
parameterized by
![]() for
for
![]() .
.
![\begin{maximasession}
F(x,y,z) := [-x*y^3, x*z, y*z^2];
[x,y,z]: [t^2, t^3, t^4]...
.... diff([x,y,z], t), t, 0, 1); \\
\o7. .4461538461603605 \\
\end{maximasession}](img223.png)