Conservative Vector Fields and Finding Scalar Potentials

We know from theory that a vector field $\mathbf{F}$ is conservative if there exists a function $f$ such that $\mathbf{F} = \nabla f$. Further, we know that fields defined on suitably nice regions are conservative if they are irrotational.

We can check whether a field is conservative with the curl function in the vect package. For example, let's check the field $\mathbf{F}(x,y)=(4x^3 - 5y^2)\mathbf{i} + (5y^3 - 3x)\mathbf{j}$.

Since the curl is not zero, the field is not conservative. How about

$$\mathbf{F}(x,y)=(x^3 + 5y)\mathbf{i} + (5y^3 + 5x)\mathbf{j}?$$

Since the curl is zero, this field is conservative. So the function $f$ satisfying $\mathbf{F} = \nabla f$ exists. We can find the scalar potential $f$ in Maxima with the potential function (also in the vect package).

Note, however, that because of a bug in Maxima at the time of this writing we need to do a little fancy footwork. We cannot use the letter x in the function call; instead we will change it to another letter. When we do that, we must follow it by a call to scalefactors.

We can easily check that $f(x,y) = (5x^4 + 20xy +y^4)/4$ satisfies $\mathbf{F} = \nabla f$. The fundamental theorem for line integrals now allows us to compute line integrals that look like

$$\int_C\mathbf{F}\cdot\mathrm{d}\mathbf{r} = \int_C \nabla f \cdot\mathrm{d}\mathbf{r},$$

which simplifies to $f(\mathbf{r}(b)) - f(\mathbf{r}(a))$. So, for instance, for a curve $C$ with initial point $(0,1)$ and terminal point $(2,3)$ we have

$$\int_C\mathbf{F}\cdot\mathrm{d}\mathbf{r} = \int_C \left[(x... ...f{i} + (5y^3 + 5x)\mathbf{j} \right] \cdot\mathrm{d}\mathbf{r}$$

to be equal to (using the result from potential, above)

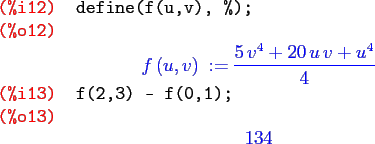
All of the above can be done in three dimensions, too. We need only to do scalefactors([x,y,z]) and scalefactors([u,v,w]), when appropriate.