Optimization and Local Extrema

To find critical points we need to solve the system of equations $f_x = 0$ and $f_y = 0$. Let $f(x,y)= 2x^4 + 2y^4 - 8xy$.

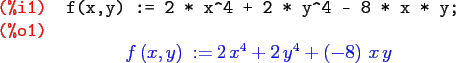
Let's take a look at a plot of $f$.

See Figure BLANK.

Figure 12: A surface plot of $f$

Now let's take a look at a contour plot of $f$. We do it just like the plot of the surface, except we use the argument contour = map.

See Figure BLANK.

Figure 13: The level curves of $f$ which suggest two extrema and a saddle point

Now let's find the first order partial derivatives of $f$, set them equal to zero, and solve for values of $(x,y)$. We do this with the solve function, which assumes that the expressions are set equal to zero by default. Keep in mind that solve finds all real and complex solutions; we only care about the real valued solutions, however, and will ignore the rest.

Critical points are at $(0,0)$, $(1,1)$, and $(-1,-1)$. (Note that both partial derivatives exist everywhere.) We need to see what the Hessian says at those locations.

We do the Second Derivative Test by plugging in the above three points into $f_{xx}$ and $\mathrm{det}(\mathrm{H})$. (Of course we can do it mentally but let's try it with Maxima.) A quick way to plug numbers into expressions is with the subst function.

From the above we conclude that $(-1,-1)$ is a local minimum of $f$, and the value is

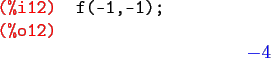
Doing the same for $(0,0)$ and $(1,1)$ shows that $(0,0)$ is a saddle point and $(1,1)$ is also a local minimum (we know this already by symmetry).