next up previous contents
Next: Linear Approximation and Differentials Up: Functions of Several Variables Previous: Functions of Several Variables   Contents

Partial Derivatives

We do partial derivatives in the natural way. For example, for the partial derivative with respect to $x$ we do


\begin{maximasession} diff(f(x,y), x); \maximaoutput* \i1. diff(f(x,y), x); \\ \o1. {{d}\over{d x}} f\left(x , y\right) \\ \end{maximasession}

The long way to get higher order derivatives is to nest the diff calls. The second order partial derivative is


\begin{maximasession} diff(diff(f(x,y), x), x); \maximaoutput* \i2. diff(diff(f(... ..., x); \\ \o2. {{d^2}\over{d x^2}} f\left(x , y\right) \\ \end{maximasession}

and the second partial with respect to $x$ then $y$ is


\begin{maximasession} diff(diff(f(x,y), x), y); \maximaoutput* \i3. diff(diff(f(... ...; \\ \o3. {{d^2}\over{d x d y}} f\left(x , y\right) \\ \end{maximasession}

For higher order partial derivatives a quicker way is to do


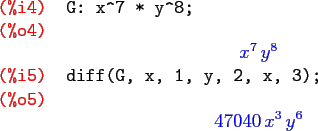
\begin{maximasession} G: x^7 * y^8; diff(G, x, 1, y, 2, x, 3); \maximaoutput* \i... ...\i5. diff(G, x, 1, y, 2, x, 3); \\ \o5. 47040 x^3 y^6 \\ \end{maximasession}

The above first differentiates $G$ with respect to $x$ three times, then with respect to $y$ two times, and finally with respect to $x$ one time; that is, the arguments match the Leibnitz notation for partial derivatives.




G. Jay Kerns 2009-12-01