Next: Vector Calculus Up: Multiple Integration Previous: Integrals in Cylindrical and Contents
For more general transformations ![]() and
and ![]() we can use the jacobian function in the linearalgebra package, which is loaded by default. Let
we can use the jacobian function in the linearalgebra package, which is loaded by default. Let ![]() , and we will calculate
, and we will calculate
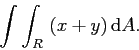
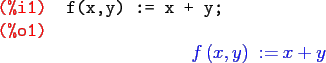
Let's make the transformation ![]() and
and ![]() .
.
![\begin{maximasession}[x,y]: [u^3 - v^4, 5 * u * v];
\maximaoutput*
\i2. [x,y]: [...
...4, 5 * u * v]; \\
\o2. \left[ u^3-v^4 , 5 u v \right] \\
\end{maximasession}](img184.png)
We need the Jacobian:
![\begin{maximasession}
J: jacobian([x,y], [u,v]);
J: determinant(J);
\maximaoutpu...
...r } \\
\i4. J: determinant(J); \\
\o4. 20 v^4+15 u^3 \\
\end{maximasession}](img185.png)
We were lucky in this example because the Jacobian is positive as long as ![]() is positive (or just not terribly negative). If this had not happened then we would need to be careful about the sign of
is positive (or just not terribly negative). If this had not happened then we would need to be careful about the sign of ![]() , which in principle could be a problem because Maxima does not integrate absolute value. Nevertheless, we finish up with the integration. It takes the form (we will make up random limits of integration, but in a given problem we would need to determine these)
, which in principle could be a problem because Maxima does not integrate absolute value. Nevertheless, we finish up with the integration. It takes the form (we will make up random limits of integration, but in a given problem we would need to determine these)


G. Jay Kerns 2009-12-01