Next: Change of Variables Up: Multiple Integration Previous: Triple Integrals Contents
Let's do an integral in cylindrical coordinates.
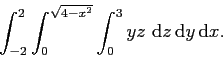
Note that ![]() goes from 0 to 2 and
goes from 0 to 2 and ![]() goes from 0 to
goes from 0 to ![]() .
.
![\begin{maximasession}
f(x,y,z) := y*z;
[x,y,z] : [r*cos(theta), r*sin(theta), z]...
...te(f(x,y,z)*r, z,0,3), r,0,2), theta,0,%pi); \\
\o3. 24 \\
\end{maximasession}](img170.png)
Now let's do an integral in spherical coordinates.

Note that ![]() goes from 0 to 1,
goes from 0 to 1, ![]() goes from 0 to
goes from 0 to ![]() , and
, and ![]() goes from 0 to
goes from 0 to ![]() .
.
![\begin{maximasession}
kill(f,x,y,z);
f(x,y,z) := x*z;
[x,y,z] : [rho*sin(phi)*co...
...,theta,0,%pi), phi,0,%pi/2); \\
\o7. {{\pi^2}\over{40}} \\
\end{maximasession}](img175.png)